POLYFIT Function in Excel

=POLYFIT(known_xs, known_ys, n)

Argument	Description	Example
known_xs	A vector of known values for x	{2;2.5;4;5.1}
known_ys	A vector of known values for y	{22.5;13;7;16}
n	Degree of the polynomial to fit	2

Download the Template

In the template file, navigate to the Polynomials worksheet to see the POLYFIT function in action.

Description

POLYFIT uses linear regression via the LINEST function to return the coefficients for a polynomial function p(x) of degree n that best fits the data provided in the x and y vectors.

The n+1 coefficients are listed in order of decreasing power {β_n, β_n-1, ... β₂, β₁, β₀} corresponding to {xⁿ, x^n-1, ... x², x¹, 1}.

Note: Linear Regression refers to solving for the coefficients of an equation of additive terms that takes this form:
Y = β_n*X_n + β_n-1*X_n-1 + … + β₂*X₂ + β₁*X₁ + β₀

When using LINEST for degrees higher than 1, it is necessary to assemble the X matrix so that each column represents a power of the original vector x. So, the POLYFIT is mostly just a convenient way of using LINEST without having to build up the X matrix yourself.

POLYFIT(known_ys,known_xs,n) = LINEST(known_ys,known_xs^SEQUENCE(1,n))

The POLYFIT function is used as the basis for many other polynomial related functions, which is another reason for defining it the way it is commonly used in software such as Matlab. The order of the coefficients in consistent with the LINEST function as well as the polyfit Matlab function.

Lambda Formula

This code for using POLYFIT in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.

Code to Create Function via the Name Manager

Name: POLYFIT
Comment: Returns the coefficients for the nth-degree polynomial fit using LINEST
Refers To:

=LAMBDA(known_xs,known_ys,n,
LET(doc,"https://www.vertex42.com/lambda/polyfit.html",
    LINEST(known_ys,known_xs^SEQUENCE(1,n))
))

Code for AFE Workbook Module (Excel Labs Add-in)

/**
* Returns the coefficients for the nth-degree polynomial fit using LINEST
*/
POLYFIT = LAMBDA(known_xs,known_ys,n,
LET(doc,"https://www.vertex42.com/lambda/polyfit.html",
    LINEST(known_ys,known_xs^SEQUENCE(1,n))
));

Named Function for Google Sheets

Name: POLYFIT
Description: Returns the coefficients for the nth-degree polynomial fit using LINEST
Arguments: known_xs, known_ys, n (see above for descriptions and example values)
Function:

LET(doc,"https://www.vertex42.com/lambda/polyfit.html",
    ARRAYFORMULA(LINEST(known_ys,known_xs^SEQUENCE(1,n)))
)

Warning

These functions are not compatible between Excel and Google Sheets. When using these functions, you will not be able to convert the Excel file to Google Sheets or vice versa without problems.

POLYFIT Examples

Example

Based on a vector of known x values and a vector of the corresponding known y values, find the coefficients for a polynomial p(x) of degree n fit using linear regression.

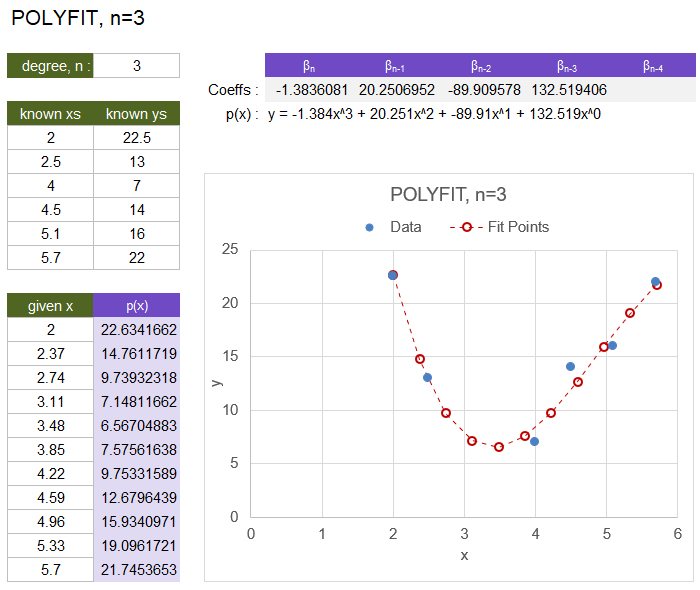
Test: Copy and Paste this LET function into a cell
=LET(
    known_xs, {2;2.5;4;4.5;5.1;5.7},
    known_ys, {22.5;13;7;14;16;22},
    n, 3,
    POLYFIT(known_xs,known_ys,n)
)

Result: {-1.384, 20.251, -89.910, 132.519}

p(x) = -1.384x^3 + 20.251x^2 + -89.910x^1 + 132.519x^0

After finding the coefficients with POLYFIT, the POLYVAL function can be used to evaluate p(x) for other values of x. The image below shows an example of fitting a 3rd-order polynomial.

Note

With a scatter plot in Excel, you can do a polynomial curve fit by adding a Trendline to your data series and choosing the Polynomial trendline option. You can display the equation on the chart, also.

Warning

For large values of x, the least squares fit (via LINEST) can become numerically unstable (likely due to rounding and/or precision errors). See the example on the PINTERP page. So, when fitting a portion of a function at large values of x, shifting the curve to start at x=0 may help avoid machine error.

POLYFIT