ISPRIME Function for Excel
=ISPRIME(n)
| Argument | Description | Example |
|---|---|---|
| number | A number or an array of numbers to check if prime. | {100,101;102,103} |
In the template file, navigate to the Sequences worksheet to see the ISPRIME function in action.
Description
The ISPRIME function determines if a number or array of numbers is prime using a reasonably efficient algorithm. It uses precomputed primes up to 997 and a reasonably optimized set of divisors for numbers beyond this range. Non-integer or negative inputs are automatically excluded as non-prime.
Examples
| Formula | Result |
|---|---|
| =ISPRIME(17) | TRUE |
| =ISPRIME(18) | FALSE |
| =ISPRIME({19,20,21;22,23,24}) | {TRUE,FALSE,FALSE; FALSE,TRUE,FALSE} |
| =ISPRIME(997) | TRUE |
| =ISPRIME(SEQUENCE(1,5,1009)) | {TRUE,FALSE,FALSE,FALSE,TRUE} |
How ISPRIME Works
A prime number is defined as a positive integer that has exactly two distinct positive divisors: 1 and itself. A valid but inefficient method for checking if a number is prime is to test all numbers 1 to SQRT(n) to see if they are divisors. The ISPRIME function uses a less brute-force method through the following modifications:
- Precomputed Primes: A precomputed list of primes up to 997 allows rapid evaluation of small numbers.
- Initial Filtering: Numbers < 2, non-integers, and even numbers > 2 are immediately excluded.
- Efficient Divisor Testing: Numbers > 997 are tested for divisibility using candidate divisors of the form 30k + i, where i is a prime offset.
Primes < 1000
The ISPRIME function uses this precomputed list of primes for numbers < 1000:
=LET(
primes,
{2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59;61;67;71;73;79;83;
89;97;101;103;107;109;113;127;131;137;139;149;151;157;163;167;173;
179;181;191;193;197;199;211;223;227;229;233;239;241;251;257;263;
269;271;277;281;283;293;307;311;313;317;331;337;347;349;353;359;
367;373;379;383;389;397;401;409;419;421;431;433;439;443;449;457;
461;463;467;479;487;491;499;503;509;521;523;541;547;557;563;569;
571;577;587;593;599;601;607;613;617;619;631;641;643;647;653;659;
661;673;677;683;691;701;709;719;727;733;739;743;751;757;761;769;
773;787;797;809;811;821;823;827;829;839;853;857;859;863;877;881;
883;887;907;911;919;929;937;941;947;953;967;971;977;983;991;997},
primes
)
Reducing Candidate Divisors
Theoretically, we only need to check the prime divisors from 2 to INT(SQRT(number)). However, if we don't already have a list of the prime divisors, we can use the fact that all primes greater than 30 are of the form 30k+i for i in {1,7,11,13,17,19,23,29}. This is based on the Primality Testing article on wikipedia (see references below).
For numbers > 997, the list of candidate divisors is generated using:
VSTACK(2,3,5,7,11,13,17,19,23,29,
TOCOL(SEQUENCE(INT((SQRT(v))/30))*30+{1,7,11,13,17,19,23,29})
)
This ensures only relevant primes and offsets are checked, improving efficiency compared to checking all integers up to SQRT(number).
Lambda Formula
This code for using ISPRIME in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.
Commented Code for AFE Workbook Module (Excel Labs Add-in)
/** * Check if a number or array of numbers is prime. */ /* * Inputs: * n: A single number, vector, or array of numbers to check for primality. * * Outputs: * Returns a TRUE/FALSE array of the same dimensions as n, where TRUE * indicates the corresponding number is prime. * * Notes: * - Handles non-numeric inputs, negative numbers, and non-integer values. * - For numbers < 1000, uses a precomputed list of primes for faster evaluation. * - For numbers ≥ 1000, uses divisors up to SQRT(n) to determine primality. * - n limited by size of arrays in Excel. Returns #NUM! when n is too large. */ ISPRIME = LAMBDA(n, LET(doc, "https://www.vertex42.com/lambda/isprime.html", version, "1/16/2025 - Updated to account for max n", // Step 1: List of primes below 1000 for fast checks. primes, {2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59;61;67;71;73;79;83;89; 97;101;103;107;109;113;127;131;137;139;149;151;157;163;167;173;179;181;191; 193;197;199;211;223;227;229;233;239;241;251;257;263;269;271;277;281;283;293; 307;311;313;317;331;337;347;349;353;359;367;373;379;383;389;397;401;409;419; 421;431;433;439;443;449;457;461;463;467;479;487;491;499;503;509;521;523;541; 547;557;563;569;571;577;587;593;599;601;607;613;617;619;631;641;643;647;653; 659;661;673;677;683;691;701;709;719;727;733;739;743;751;757;761;769;773;787; 797;809;811;821;823;827;829;839;853;857;859;863;877;881;883;887;907;911;919; 929;937;941;947;953;967;971;977;983;991;997}, // Step 2: Evaluate each number in the input array. MAKEARRAY(ROWS(n), COLUMNS(n), LAMBDA(i, j, LET(v, INDEX(n, i, j), // Step 3: Check to exclude obvious non-prime candidates. IF( OR( NOT(ISNUMBER(v)), v<2, INT(v)<>v, AND(v<>2, ISEVEN(v)) ), FALSE, IF( v < 1000, // Step 4: If v < 1000, check against list ISNUMBER(XMATCH(v, primes, 0)), // Step 5: Otherwise, test divisors LET( test_divisors, VSTACK(2,3,5,7,11,13,17,19,23,29, TOCOL(SEQUENCE(INT((SQRT(v))/30))*30 + {1,7,11,13,17,19,23,29}) ), MIN(MOD(v/test_divisors,1))>0 ) ) ) ) )) ));
For this particular algorithm, the maximum size allowed for n is limited by the size of arrays in Excel. There are 1024^2 rows in Excel, and if we are testing divisors up to SQRT(n), that means the maximum n is approximately 1024^4 (approximate because we are limiting the divisors further by using forms 30k+i). It can actually test the 42,000,000,000th prime, which is 1121614951687 (slightly larger than 1024^4).
The new algorithm (as of 1/16/2025) returns #NUM! for large numbers that need to use the test_divisors part of the algorithm. This is because SEQUENCE cannot produce a large enough array of divisors. Example: To test this limit, try entering =SEQUENCE(1E15) in Excel. The current maximum appears to be SEQUENCE(1025^4), even when used within LET and LAMBDA.
Primes Numbers Less than 10000
I tested the above function against the following list of primes less than 10000 (which were found using a more brute-force method).
=LET(primes, {2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59; 61;67;71;73;79;83;89;97;101;103;107;109;113;127;131;137;139;149;151; 157;163;167;173;179;181;191;193;197;199;211;223;227;229;233;239;241; 251;257;263;269;271;277;281;283;293;307;311;313;317;331;337;347;349; 353;359;367;373;379;383;389;397;401;409;419;421;431;433;439;443;449; 457;461;463;467;479;487;491;499;503;509;521;523;541;547;557;563;569; 571;577;587;593;599;601;607;613;617;619;631;641;643;647;653;659;661; 673;677;683;691;701;709;719;727;733;739;743;751;757;761;769;773;787; 797;809;811;821;823;827;829;839;853;857;859;863;877;881;883;887;907; 911;919;929;937;941;947;953;967;971;977;983;991;997;1009;1013;1019; 1021;1031;1033;1039;1049;1051;1061;1063;1069;1087;1091;1093;1097;1103; 1109;1117;1123;1129;1151;1153;1163;1171;1181;1187;1193;1201;1213;1217; 1223;1229;1231;1237;1249;1259;1277;1279;1283;1289;1291;1297;1301;1303; 1307;1319;1321;1327;1361;1367;1373;1381;1399;1409;1423;1427;1429;1433; 1439;1447;1451;1453;1459;1471;1481;1483;1487;1489;1493;1499;1511;1523; 1531;1543;1549;1553;1559;1567;1571;1579;1583;1597;1601;1607;1609;1613; 1619;1621;1627;1637;1657;1663;1667;1669;1693;1697;1699;1709;1721;1723; 1733;1741;1747;1753;1759;1777;1783;1787;1789;1801;1811;1823;1831;1847; 1861;1867;1871;1873;1877;1879;1889;1901;1907;1913;1931;1933;1949;1951; 1973;1979;1987;1993;1997;1999;2003;2011;2017;2027;2029;2039;2053;2063; 2069;2081;2083;2087;2089;2099;2111;2113;2129;2131;2137;2141;2143;2153; 2161;2179;2203;2207;2213;2221;2237;2239;2243;2251;2267;2269;2273;2281; 2287;2293;2297;2309;2311;2333;2339;2341;2347;2351;2357;2371;2377;2381; 2383;2389;2393;2399;2411;2417;2423;2437;2441;2447;2459;2467;2473;2477; 2503;2521;2531;2539;2543;2549;2551;2557;2579;2591;2593;2609;2617;2621; 2633;2647;2657;2659;2663;2671;2677;2683;2687;2689;2693;2699;2707;2711; 2713;2719;2729;2731;2741;2749;2753;2767;2777;2789;2791;2797;2801;2803; 2819;2833;2837;2843;2851;2857;2861;2879;2887;2897;2903;2909;2917;2927; 2939;2953;2957;2963;2969;2971;2999;3001;3011;3019;3023;3037;3041;3049; 3061;3067;3079;3083;3089;3109;3119;3121;3137;3163;3167;3169;3181;3187; 3191;3203;3209;3217;3221;3229;3251;3253;3257;3259;3271;3299;3301;3307; 3313;3319;3323;3329;3331;3343;3347;3359;3361;3371;3373;3389;3391;3407; 3413;3433;3449;3457;3461;3463;3467;3469;3491;3499;3511;3517;3527;3529; 3533;3539;3541;3547;3557;3559;3571;3581;3583;3593;3607;3613;3617;3623; 3631;3637;3643;3659;3671;3673;3677;3691;3697;3701;3709;3719;3727;3733; 3739;3761;3767;3769;3779;3793;3797;3803;3821;3823;3833;3847;3851;3853; 3863;3877;3881;3889;3907;3911;3917;3919;3923;3929;3931;3943;3947;3967; 3989;4001;4003;4007;4013;4019;4021;4027;4049;4051;4057;4073;4079;4091; 4093;4099;4111;4127;4129;4133;4139;4153;4157;4159;4177;4201;4211;4217; 4219;4229;4231;4241;4243;4253;4259;4261;4271;4273;4283;4289;4297;4327; 4337;4339;4349;4357;4363;4373;4391;4397;4409;4421;4423;4441;4447;4451; 4457;4463;4481;4483;4493;4507;4513;4517;4519;4523;4547;4549;4561;4567; 4583;4591;4597;4603;4621;4637;4639;4643;4649;4651;4657;4663;4673;4679; 4691;4703;4721;4723;4729;4733;4751;4759;4783;4787;4789;4793;4799;4801; 4813;4817;4831;4861;4871;4877;4889;4903;4909;4919;4931;4933;4937;4943; 4951;4957;4967;4969;4973;4987;4993;4999;5003;5009;5011;5021;5023;5039; 5051;5059;5077;5081;5087;5099;5101;5107;5113;5119;5147;5153;5167;5171; 5179;5189;5197;5209;5227;5231;5233;5237;5261;5273;5279;5281;5297;5303; 5309;5323;5333;5347;5351;5381;5387;5393;5399;5407;5413;5417;5419;5431; 5437;5441;5443;5449;5471;5477;5479;5483;5501;5503;5507;5519;5521;5527; 5531;5557;5563;5569;5573;5581;5591;5623;5639;5641;5647;5651;5653;5657; 5659;5669;5683;5689;5693;5701;5711;5717;5737;5741;5743;5749;5779;5783; 5791;5801;5807;5813;5821;5827;5839;5843;5849;5851;5857;5861;5867;5869; 5879;5881;5897;5903;5923;5927;5939;5953;5981;5987;6007;6011;6029;6037; 6043;6047;6053;6067;6073;6079;6089;6091;6101;6113;6121;6131;6133;6143; 6151;6163;6173;6197;6199;6203;6211;6217;6221;6229;6247;6257;6263;6269; 6271;6277;6287;6299;6301;6311;6317;6323;6329;6337;6343;6353;6359;6361; 6367;6373;6379;6389;6397;6421;6427;6449;6451;6469;6473;6481;6491;6521; 6529;6547;6551;6553;6563;6569;6571;6577;6581;6599;6607;6619;6637;6653; 6659;6661;6673;6679;6689;6691;6701;6703;6709;6719;6733;6737;6761;6763; 6779;6781;6791;6793;6803;6823;6827;6829;6833;6841;6857;6863;6869;6871; 6883;6899;6907;6911;6917;6947;6949;6959;6961;6967;6971;6977;6983;6991; 6997;7001;7013;7019;7027;7039;7043;7057;7069;7079;7103;7109;7121;7127; 7129;7151;7159;7177;7187;7193;7207;7211;7213;7219;7229;7237;7243;7247; 7253;7283;7297;7307;7309;7321;7331;7333;7349;7351;7369;7393;7411;7417; 7433;7451;7457;7459;7477;7481;7487;7489;7499;7507;7517;7523;7529;7537; 7541;7547;7549;7559;7561;7573;7577;7583;7589;7591;7603;7607;7621;7639; 7643;7649;7669;7673;7681;7687;7691;7699;7703;7717;7723;7727;7741;7753; 7757;7759;7789;7793;7817;7823;7829;7841;7853;7867;7873;7877;7879;7883; 7901;7907;7919;7927;7933;7937;7949;7951;7963;7993;8009;8011;8017;8039; 8053;8059;8069;8081;8087;8089;8093;8101;8111;8117;8123;8147;8161;8167; 8171;8179;8191;8209;8219;8221;8231;8233;8237;8243;8263;8269;8273;8287; 8291;8293;8297;8311;8317;8329;8353;8363;8369;8377;8387;8389;8419;8423; 8429;8431;8443;8447;8461;8467;8501;8513;8521;8527;8537;8539;8543;8563; 8573;8581;8597;8599;8609;8623;8627;8629;8641;8647;8663;8669;8677;8681; 8689;8693;8699;8707;8713;8719;8731;8737;8741;8747;8753;8761;8779;8783; 8803;8807;8819;8821;8831;8837;8839;8849;8861;8863;8867;8887;8893;8923; 8929;8933;8941;8951;8963;8969;8971;8999;9001;9007;9011;9013;9029;9041; 9043;9049;9059;9067;9091;9103;9109;9127;9133;9137;9151;9157;9161;9173; 9181;9187;9199;9203;9209;9221;9227;9239;9241;9257;9277;9281;9283;9293; 9311;9319;9323;9337;9341;9343;9349;9371;9377;9391;9397;9403;9413;9419; 9421;9431;9433;9437;9439;9461;9463;9467;9473;9479;9491;9497;9511;9521; 9533;9539;9547;9551;9587;9601;9613;9619;9623;9629;9631;9643;9649;9661; 9677;9679;9689;9697;9719;9721;9733;9739;9743;9749;9767;9769;9781;9787; 9791;9803;9811;9817;9829;9833;9839;9851;9857;9859;9871;9883;9887;9901; 9907;9923;9929;9931;9941;9949;9967;9973}, primes )
Function for Returning a Sequence of Primes
The following lambda function uses the list of primes above to return the first n primes, or the primes between two values.
/** * Primes(n) returns the first n prime numbers less than 10000. * Primes(,100,200) returns all prime numbers within [100,200]. * Primes(n,10,50) returns the first n primes within [10,50] sorted in ascending order. * Primes(-n,10,50) returns the last n primes within [10,50] sorted in descending order. */ /* * Inputs: * [n]: Optional. Number of primes to return. Defaults to all primes within the range [gte, lte]. * [gte]: Optional. Lower bound of the range. Defaults to 0. * [lte]: Optional. Upper bound of the range. Defaults to 10000. * * Outputs: * Returns an array of prime numbers based on the input parameters: * - If n is omitted, returns all primes in [gte, lte]. * - If n > 0, returns the first n primes in ascending order. * - If n < 0, returns the last n primes in descending order. * * Notes: * - Relies on the variable `the_array_of_primes_lt_10000`, which should contain all primes < 10000. * - Uses the FILTER function to narrow results to the specified range. */ Primes = LAMBDA([n], [gte], [lte], LET(doc, "https://www.vertex42.com/lambda/isprime.html", // Step 1: Handle default values for optional parameters. lte, IF(ISOMITTED(lte), 10000, lte), gte, IF(ISOMITTED(gte), 0, gte), // Step 2: Define the array of primes and handle n defaults. array, the_array_of_primes_lt_10000, n, IF(ISOMITTED(n), ROWS(array), n), // Step 3: Filter primes within the range [gte, lte]. filtered, FILTER( array, 1*(array <= lte) * (array >= gte) ), // Step 4: Return the first n or last n primes based on the sign of n. IF( n < ROWS(filtered), SORT( TAKE(filtered, n, 1), 1, SIGN(n)*1 ), filtered ) ));
Divisors and Prime Factorization
A discussion on LinkedIn with Mehmet Çiçek led to the following related functions, which can be used to get a list of all the divisors and then the prime factorization for a number (limited to less than 1024^4).
/** * Returns the Prime Factorization from a list of all divisors * See the AllDivisors function. */ PrimeFactorization = LAMBDA(number, divisors, LET(doc,"https://www.vertex42.com/lambda/isprime.html", credit,"ChatGPT with help", primes, FILTER(divisors, ISPRIME(divisors)), Factorize, LAMBDA(F, n, primes, factors, LET( // Find the first prime that divides n divisor, XMATCH(TRUE, MOD(n, primes) = 0), // Check if no more factors exist is_done, ISNA(divisor), // Get the prime factor and calculate the remaining quotient prime, INDEX(primes, divisor), quotient, n / prime, // Update the list of factors and recurse if needed new_factors, IF(is_done, factors, VSTACK(factors, prime)), // Recurse if the quotient is greater than 1 IF(is_done, factors, F(F, quotient, primes, new_factors)) )), prime_factors, DROP(Factorize(Factorize, number, primes, ""),1), TOCOL(prime_factors) ));
/** * Returns a list of all Divisors of a number * number limited to < 1024^4 due to size of arrays in Excel */ AllDivisors = LAMBDA(number, LET(doc,"https://www.vertex42.com/lambda/isprime.html", credit,"Mehmet Çiçek and ChatGPT", seq,SEQUENCE(INT(SQRT(number))), div,TOCOL(IFS(MOD(number,seq)=0,seq),3), SORT(UNIQUE(VSTACK(div,number/div))) ));
Sieve of Eratosthenes
One of the best ways to find all of the primes less than some number n is to use the Sieve of Eratosthenes algorithm. At its core, the algorithm is quite simple, and I was given the following lambda code by Danny Whittaker which demonstrates it. This lambda is meant more as a starting point and educational tool. There are ways to make the algorithm more efficient, such as starting with a smaller set of prime candidates.
/** * SIEVE(n) returns the prime numbers up to n using a * Sieve of Eratosthenes algorithm. */ SIEVE = LAMBDA(n, LET(source, "Danny Whittaker", // Initial Candidates: all numbers starting with 2 nums, SEQUENCE(n-1, 1, 2), // Sieve of Eratosthenes algorithm REDUCE(nums, SEQUENCE(INT(SQRT(n))), LAMBDA(seq, i, LET( // Select the current factor (smallest remaining number) factor, INDEX(seq, i), // Filter out multiples of the selected factor // Keeping the current factor (because it is prime) FILTER(seq, (MOD(seq, factor) > 0) + (seq = factor) ) ) ) ) ));
The image below shows visually what is going on which each iteration of the algorithm.
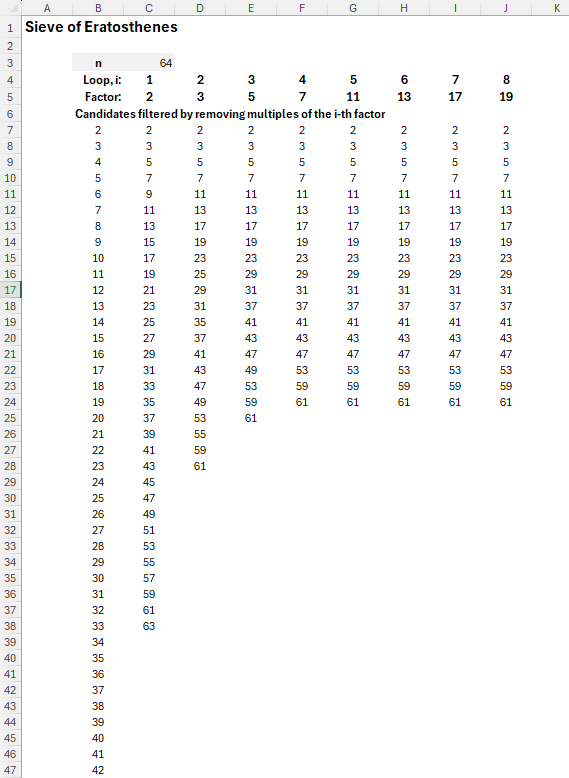 How the SIEVE of Eratosthenes algorithm works
How the SIEVE of Eratosthenes algorithm worksRevision History
- 1/16/2025: Refined ISPRIME code and modified to produce errors when n is too large. Previous bug returned FALSE for large number (>1024^4). It should now return #NUM! errors for numbers that are too large.
