L_CHOLESKY

=L_CHOLESKY(matrix)

Download the Template

In the template file, navigate to the Matrices worksheet to see the L_CHOLESKY function in action.

Description

Cholesky decomposition or factorization is a method in linear algebra used to solve linear systems of equations, when the matrix satisfies the conditions of being symmetric and positive-definite. You can use the isSymmetric function to check that A=TRANSPOSE(A), and isPositiveDefinite to check if all upper-left determinants are greater than zero.

The L_CHOLESKY function returns the lower triangle matrix L where A = LL^T or A=MMULT(L,TRANSPOSE(L)). If you want the upper triangle matrix, use can use TRANSPOSE(L_CHOLESKY(matrix)).

Cholesky decomposition is used in numerous applications including finite element analysis, Kalman filters, Monte Carlo Simulation (for generating correlated random variables), and optimization. The Cholesky algorithm is very efficient when the conditions are met. When the matrix is not symmetric, consider using LU Decomposition.

How it Works

L_CHOLESKY first checks the necessary conditions and then uses the REDUCE function to gradually build the L matrix one column at a time. You can think of REDUCE as a for-loop that sequentially adds a new column to L and increments the column number j from 1 to n.

VSTACK is used to asemble each column as {0;L_jj;L_ij}. VSTACK cannot accept empty arrays, so for j=1 we stack {L_jj;L_ij} and for j=n we stack {0;L_jj}.

This function is the closest I was able to get to reproducing the vectorized version of the Cholesky-Crout algorithm, which starts in the upper-left corner and creates the L matrix one column at a time using a dot product for L_jj and matrix multiplication for L_ij.

To see the algorithm step-by-step, you can refer to the LAMBDA library template file which includes the L_CHOL example calculated cell-by-cell using the same procedure as in the LAMBDA function.

LDL Decomposition can be done using a very similar algorithm. The function for LDL decomposition is available upon request.

Lambda Formula

This code for using L_CHOLESKY in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.

/**
* Returns the Cholesky decomposition for a symmetric positive-definite matrix
*/
L_CHOLESKY = LAMBDA(matrix,
LET(doc,"https://www.vertex42.com/lambda/cholesky.html",
    n,ROWS(matrix),
    IF(ROWS(matrix)<>COLUMNS(matrix),
        "Error: matrix not square",
    IF(SUM(--(matrix<>TRANSPOSE(matrix)))<>0,
        "Error: not symmetric",
    IF(MDETERM(matrix)<=0,
        "Error: not positive definite",
    REDUCE(0,SEQUENCE(n),LAMBDA(Lmat,j,
        IF(j=1,
            LET(Ljj,SQRT(INDEX(matrix,j,j)),
                Lij,CHOOSEROWS(INDEX(matrix,0,1),SEQUENCE(n-1,1,2,1))/Ljj,
                VSTACK(Ljj,Lij)
            ),
        IF(j=n,
            LET(Ljj,SQRT(INDEX(matrix,j,j)-SUM(CHOOSEROWS(Lmat,j)^2)),
                HSTACK(Lmat,VSTACK(SEQUENCE(n-1,1,0,0),Ljj))
            ),
            LET(Ljj,SQRT(INDEX(matrix,j,j)-SUM(CHOOSEROWS(Lmat,j)^2)),
                Aij,CHOOSEROWS(INDEX(matrix,0,j),SEQUENCE(n-j,1,j+1,1)),
                Lik,CHOOSEROWS(Lmat,SEQUENCE(n-j,1,j+1,1)),
                Ljk,CHOOSEROWS(Lmat,j),
                Lij,1/Ljj*(Aij-MMULT(Lik,TRANSPOSE(Ljk))),
                HSTACK(Lmat,VSTACK(SEQUENCE(j-1,1,0,0),Ljj,Lij))
            )
        ))
    ))
    )))
));

Name: L_CHOLESKY
Description: Cholesky decomposition of a symmetric positive-definite matrix
Arguments: matrix
Function:

=LET(doc,"https://www.vertex42.com/lambda/cholesky.html",
n,ROWS(matrix),
IF(ROWS(matrix)<>COLUMNS(matrix),"Error: matrix not square",
IF(ARRAYFORMULA(SUM(--(matrix<>TRANSPOSE(matrix)))<>0),"Error: not symmetric",
IF(MDETERM(matrix)<=0,"Error: not positive definite",
REDUCE(0,SEQUENCE(n),LAMBDA(Lmat,j,
IF(j=1,LET(Ljj,SQRT(INDEX(matrix,j,j)),
  Lij,ARRAYFORMULA(CHOOSEROWS(INDEX(matrix,0,1),SEQUENCE(n-1,1,2,1))/Ljj),
  VSTACK(Ljj,Lij)),
IF(j=n,LET(Ljj,ARRAYFORMULA(SQRT(INDEX(matrix,j,j)-SUM(CHOOSEROWS(Lmat,j)^2))),
  HSTACK(Lmat,VSTACK(SEQUENCE(n-1,1,0,0),Ljj))),
LET(Ljj,ARRAYFORMULA(SQRT(INDEX(matrix,j,j)-SUM(CHOOSEROWS(Lmat,j)^2))),
  Aij,CHOOSEROWS(INDEX(matrix,0,j),SEQUENCE(n-j,1,j+1,1)),
  Lik,CHOOSEROWS(Lmat,SEQUENCE(n-j,1,j+1,1)),
  Ljk,CHOOSEROWS(Lmat,j),
  Lij,ARRAYFORMULA(1/Ljj*(Aij-MMULT(Lik,TRANSPOSE(Ljk)))),
  HSTACK(Lmat,VSTACK(SEQUENCE(j-1,1,0,0),Ljj,Lij))
)))))))))

L_CHOLESKY Examples

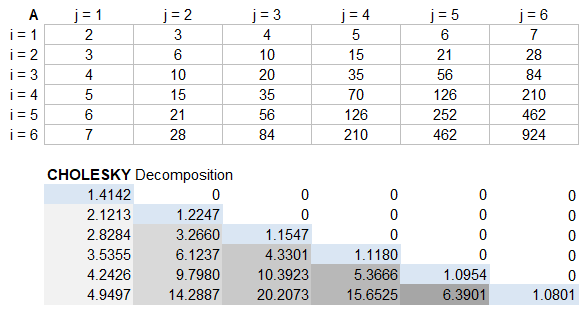
Test: Copy and Paste this LET function into a cell
=LET(
    matrix, DROP(L_PASCAL(7),1,1),
    L_CHOLESKY(matrix)
)

Result: [as shown in image above]

=LET(
    matrix, {4,12,-16;12,37,-43;-16,-43,98},
    L_CHOLESKY(matrix)
)

Result: {2,0,0;6,1,0;-8,5,3}