DIFF Function for Excel

=L_DIFF(x, [n])

Argument	Description	Example
x	A column vector, or array of column vectors	{1;3;7}
n	(default=1) The number of times to sequentially calculate the difference	1

Download the Template

In the template file, navigate to the Calc worksheet to see the L_DIFF function in action.

Description

L_DIFF returns the difference between adjacent values in a column vector: \({\Delta}x = x_{i+1}-x_i\). This can be accomplished with the DROP function in Excel like this:

L_DIFF(x) = DROP(x,1)-DROP(x,-1)

Example:

=LET(
    x, {1; 2; 4; 7; 11; 16},
    L_DIFF(x)
)

Result: {1; 2; 3; 4; 5}

The x parameter can be a single column vector, or an array of column vectors (of the same size). For example, if we have a table consisting of a column of x values and a column of y values, L_DIFF(table) would return Δx as the first column and Δy as the second column. The difference operator works separately on each column.

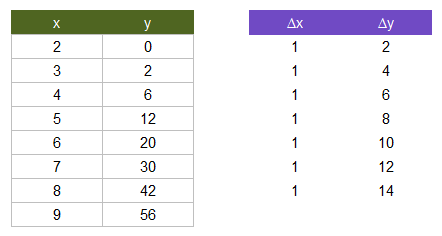
The function returns an error if the number of rows is equal to 1, so use TRANSPOSE(L_DIFF(TRANSPOSE(x))) if you want to apply L_DIFF to a row vector.

For approximating numerical derivatives, L_DIFF is meant to represent the difference operator Δ applied to discrete values using a forward difference, or \(x_{i+1}-x_i\). The resulting array has one less row, meaning that if x has m rows, then L_DIFF(x) will have m-1 rows.

Even though the difference operator has application to approximating derivatives, note that L_DIFF itself is not a derivative. Instead, a forward difference derivative would be Δy/Δx, or L_DIFF(vector_y)/L_DIFF(vector_x).

Calculating the n-th Difference

Specifying a value of n (valid only for n being an integer >= 1) will cause L_DIFF(x) to be run sequentially n times (the array loses 1 row each time). For example, L_DIFF(x,2) is the same as L_DIFF(L_DIFF(x)). Although this can be used in procedures for estimating higher-order derivatives, there may be better methods for estimating derivatives at specific values of x.

Both Matlab and Python NumPy have a similar function named diff, which is the reason for choosing this name for the LAMBDA Library.

Lambda Formula

This code for using L_DIFF in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.

Code for AFE Workbook Module (Excel Labs Add-in)

L_DIFF = LAMBDA(x,[n],
LET(doc,"https://www.vertex42.com/lambda/diff.html",
    n,IF(ISBLANK(n),1,n),
    REDUCE(1,SEQUENCE(n),LAMBDA(acc,i,
        IF(i=1,
            DROP(x,1)-DROP(x,-1),
            DROP(acc,1)-DROP(acc,-1)
        )
    ))
));

Named Function for Google Sheets

Name: L_DIFF
Description: Calculate the difference between adjacent values of a column vector
Arguments: x, n
Function:

=LET(doc,"https://www.vertex42.com/lambda/diff.html",
    n,IF(ISBLANK(n),1,n),
    REDUCE(1,SEQUENCE(n),LAMBDA(acc,i,
        IF(i=1,
            ARRAYFORMULA(L_DROP(x,1,0)-L_DROP(x,-1,0)),
            ARRAYFORMULA(L_DROP(acc,1,0)-L_DROP(acc,-1,0))
        )
    ))
)

L_DIFF Examples

Example 1: Check for Uniform Spacing

The L_ISUNIFORM function uses a forward difference to calculate the spacing between each value. It then uses the UNIQUE function to check how many different values are returned. It uses more logic than that, but consider this example where L_LINSPACE(1,10,6) = {1; 2.8; 4.6; 6.4; 8.2; 10}.

Test: Copy and Paste this LET function into a cell
=LET(
    seq, L_LINSPACE(1,10,6),
    UNIQUE(L_DIFF(seq))
)

Result: {1.800000000000000;1.800000000000000}

With uniform spacing produced by LINSPACE, using UNIQUE should have resulted in a single value 1.8. The above result indicates that Excel thought these two numbers were different because UNIQUE returned two values even though they appear to be exactly the same (note that Excel displays up to 15 digits of precision). However, if you evaluate the difference twice, the machine error becomes apparent:

=LET(
    seq, L_LINSPACE(1,10,6),
    L_DIFF(seq,2)
)

Result: {0; 0; 0; 8.88178E-16}

Now, try hard-coding the values for the sequence instead of using L_LINSPACE. It is readily apparent that the 1st difference between each value should be exactly 1.8. However, this example shows how floating-point arithmetic is not exact.

LET(
    seq, {1; 2.8; 4.6; 6.4; 8.2; 10},
    L_DIFF(seq,2)
)

Result: {0; 8.88178E-16; -1.77636E-15; 1.77636E-15}

If you have been using a budget spreadsheet for long enough without rounding, you will eventually find that your numbers can be off by a tiny 0.000000000000001. Machine precision is a reason for this. See the article floating-point arithmetic for more details about Excel precision.

Example 2: ΔFibonacci

The Fibonacci Sequence has an interesting characteristic that if you drop the first value, the forward difference is equal to the same sequence.

Test: Copy and Paste this LET function into a cell
=LET(
    fib, DROP({0;1;1;2;3;5;8;13;21;34},1),
    L_DIFF(fib)
)

Result: {0,1,1,2,3,5,8,13,21}

L_DIFF